Sentaurus Device
5. Unified Interface for Optical Generation Calculation

5.1 Integrating Optics Into Sentaurus Device
5.2 Calculating Wavelength-Dependent Reflection by TMM
5.3 Calculating Angular-Dependent Reflection Using Raytracing
5.4 Calculating the White Light Photocurrent of a 3D Photodiode Using Raytracing

Objectives

5.1 Integrating Optics Into Sentaurus Device

Sentaurus Device allows you to calculate the optical charge generation using different solvers, such as the transfer matrix method (TMM), raytracing, OptBeam (Beer's law), and the beam propagation method (BPM), or to load external generation profiles, for example, calculated by Sentaurus Device Electromagnetic Wave Solver.

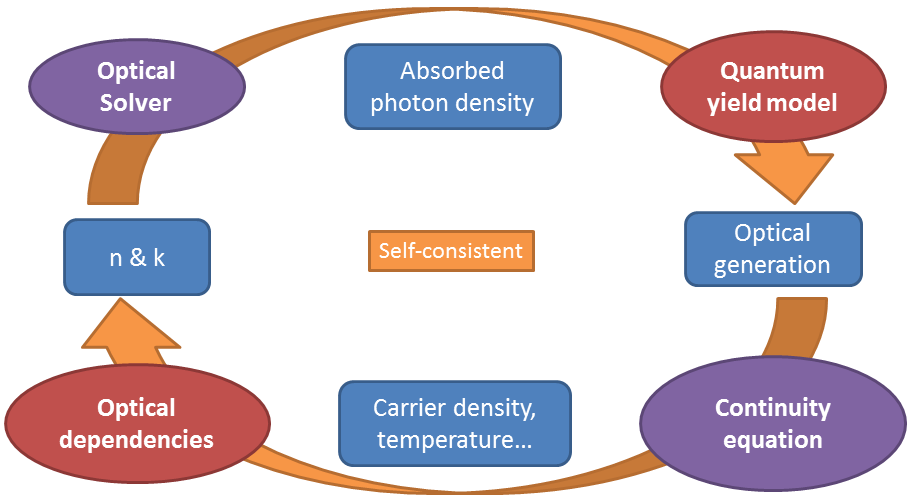
Regardless of the chosen optical solver, the Sentaurus Device setup for optics and the procedure for coupling optical generation to electronics are identical (see Figure 1).

Flow of optical and electrical device simulation

Figure 1. Simulation flow of optical device simulation. (Click image for full-size view.)

For example, for a region in the simulation domain, you can specify the refractive index (n) and the extinction coefficient (k) using different complex refractive index models, such as constant, wavelength dependent, temperature dependent, carrier dependent, or user defined. Based on the n&k values, the selected optical solver calculates the absorbed photon density, which at each vertex gives the number of absorbed photons per volume and seconds.

After choosing a suitable quantum yield model, you define how the absorbed photon density is converted to the optical generation rate. The complexity of the quantum yield model ranges from a simplistic model (unity) that assumes that each absorbed photon generates one electron–hole pair, to complex models (effectiveAbsorption) that account for free carrier absorption. A physical model interface is available to specify even more complicated user-defined models.

Then, the optical generation is added to the continuity equation. Therefore, all other equations can be solved self-consistently with that optical generation. Depending on the chosen complex refractive index model, n&k values might be dependent on temperature or carrier density. In that case, the above-described steps are repeated until convergence is achieved. However, in most cases, for passive devices, the influence of temperature and carrier density on n&k values is weak, such that the cycle is evaluated only once.

5.2 Calculating Wavelength-Dependent Reflection by TMM

This section explains the fundamental features of the unified interface for optical generation computation. As an example, the wavelength-dependent reflection of a planar silicon substrate, coated with a single silicon nitride (SiN) layer, is calculated using the transfer matrix method (TMM). The calculation is purely optical; no electrical equations are solved. Therefore, the optical generation is not of interest here.

The complete project can be investigated from within Sentaurus Workbench in the directory Applications_Library/GettingStarted/sdevice/opto/tmm-spectral-reflection.

All settings for optics are defined in an Optics(...) section inside the global Physics section. The settings inside the Optics section, in turn, can be categorized as common to all solvers such as ComplexRefractiveIndex(...), OpticalGeneration(...), and Excitation(...) or as a solver-specific section such as OpticalSolver(...).

In the following sections, you will work through all the specific settings of the example.

5.2.1 ComplexRefractiveIndex Section

The appropriate model for the n&k values must be specified in the Sentaurus Device command file.

Click to view the command file sdevice_des.cmd.

In this case, for SiN, you want to use a constant refractive index of n=2.74 with no absorption (k=0) and, for silicon, wavelength-dependent tabulated values for n (real part of the refractive index) and k (imaginary part of the refractive index) will be used, which are activated in the command file with the following line:

    ComplexRefractiveIndex (WavelengthDep(Real Imag))

The values themselves are defined in the parameter file sdevice.par of Sentaurus Device in the corresponding ComplexRefractiveIndex sections.

The keyword Formula switches the source from where the wavelength-dependent values are read:

The constant refractive index for SiN uses Formula=0:

Material = "Nitride" {
  ComplexRefractiveIndex {
    n_0	= 2.74	# [1]
    k_0	= 0.0	# [1]
    Formula = 0
  }
}

However, for silicon, tabulated values are used:

Material = "Silicon" { 
  ComplexRefractiveIndex {
    n_0	= 3.45	# [1]
    k_0	= 0.0	# [1]
    Cn_temp	= 2.0000e-04	# [K^-1]
    Cn_carr	= 1	# [1]
    Ck_carr	= 0.0000e+00 ,	0.0000e+00	# [cm^2]
    Gamma_k_carr	= 1 ,	1	# [1]
    Cn_gain	= 0.0000e+00	# [1]
    Npar	= 1.0000e+18	# [cm^-3]
    Formula = 1
    NumericalTable ( 
      # wavelength [um]  n [1] k [1];
      0.1908	0.84	2.73;
      0.1984	0.968	2.89;
      ...
    )
  }
}

It is important to note that only these coefficients are used, for which a model has been activated in the command file. For example, although the temperature dependency coefficient Cn_temp is specified, it is not used here because TemperatureDep is omitted in the ComplexRefractiveIndex section of the command file.

5.2.2 OpticalGeneration Section

The OpticalGeneration section defines how the optical generation is calculated and from which source the profiles are used. The available options are:

The last option is the appropriate source in this case, since you want to sweep through a monochromatic light source to extract the reflection for each wavelength:

    OpticalGeneration ( ComputeFromMonochromaticSource )

5.2.3 Excitation Section

In the Excitation section, everything concerning illumination including light direction, polarization, wavelength, and illumination window is set:

    Excitation (
      Wavelength = @wstart@  *[um]
      theta = 0 * angle of incidence from +y to +x axis
                * 0 points in +y direction, 90 in +x direction. 
      Intensity = 0.1 *[W/cm2]
      Polarization = 0.5 * TE, TM or a number P 0..1 where P = I_TE/I_tot  
      Window(
        Origin=(0,-@dSiN@)
        Line(x1=0 x2=1)
      )
    ) * end excitation

The wavelength is set to the Sentaurus Workbench parameter @wstart@ with a value of 0.3 μm and is used as the start wavelength here. Ramping of the wavelength can be performed in the Solve section later.

The excitation direction is defined with respect to the global coordinate system (GCS) given by the grid. It is set with theta=0 to point into the +y-direction (see Figure 6, left). The second angle for setting the excitation direction (phi) is not used in two dimensions. The illumination intensity is arbitrary here as the reflection is a relative value. The polarization defines the part of the TE polarized light and is set to 0.5, which means that both TE and TM polarization are present in equal parts.

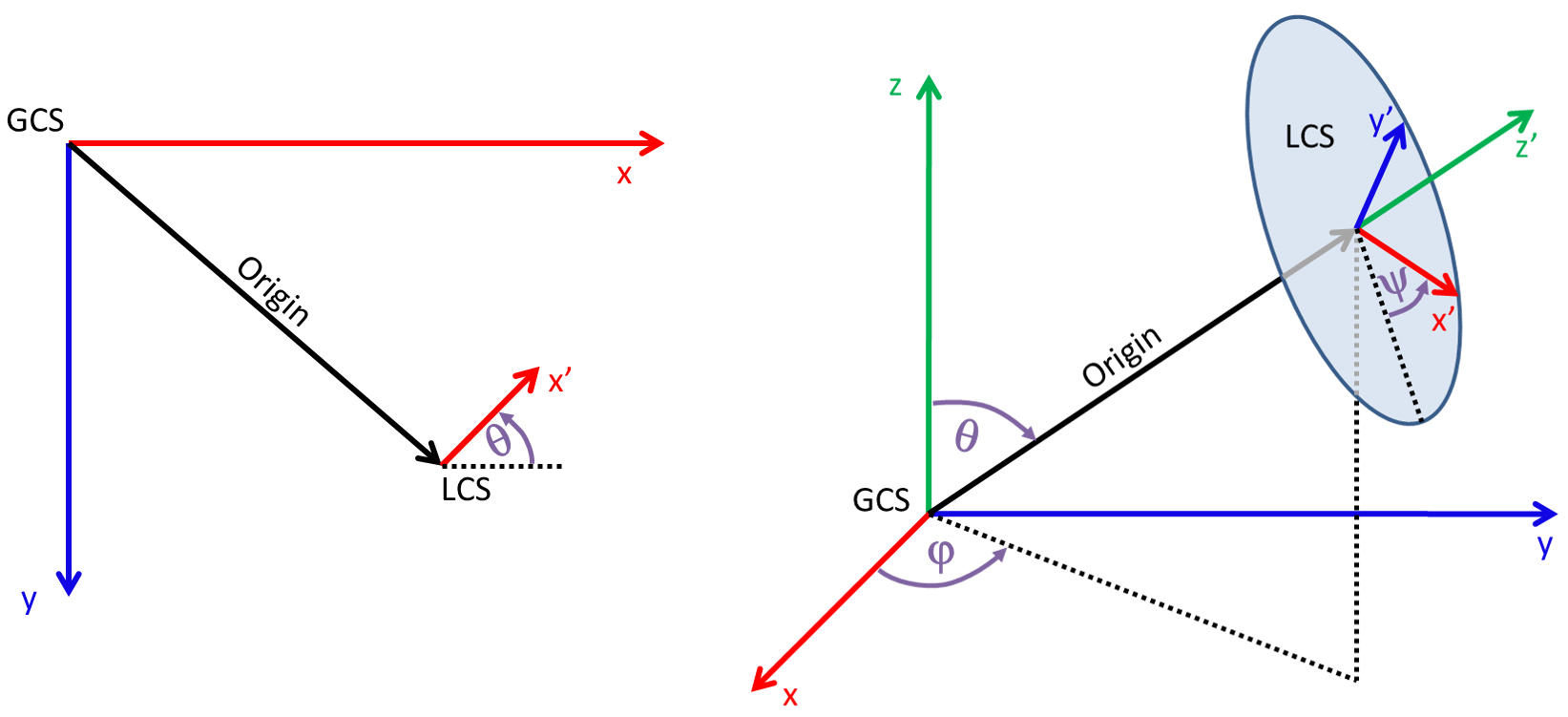
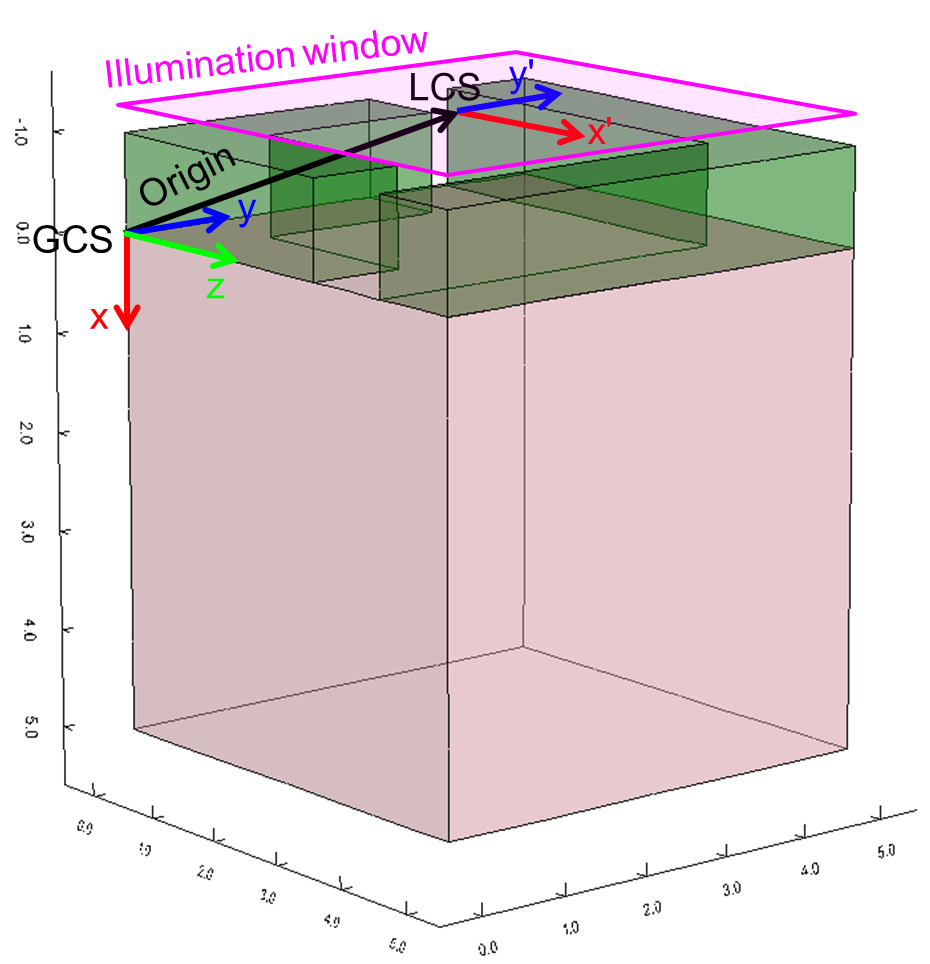
An illumination window defines the area where light falls onto the device. It is defined with the Window(...) command. For convenience, the plane of the illumination window is specified in a local coordinate system (LCS), which you can shift and rotate with respect to the GCS (see Figure 2). Actually, the LCS is a plane (x', y') in three dimensions. In two dimensions, the LCS is a line (x').

LCS in respect to GCS in two and three dimensions

Figure 2. Definition of the LCS with respect to the GCS in (left) two dimensions and (right) three dimensions. (Click image for full-size view.)

The offset of the LCS origin with respect to the GCS is controlled with the keyword Origin=(<x>, <y>). By default, Origin=(0, 0), that is, the LCS is equal to the GCS.

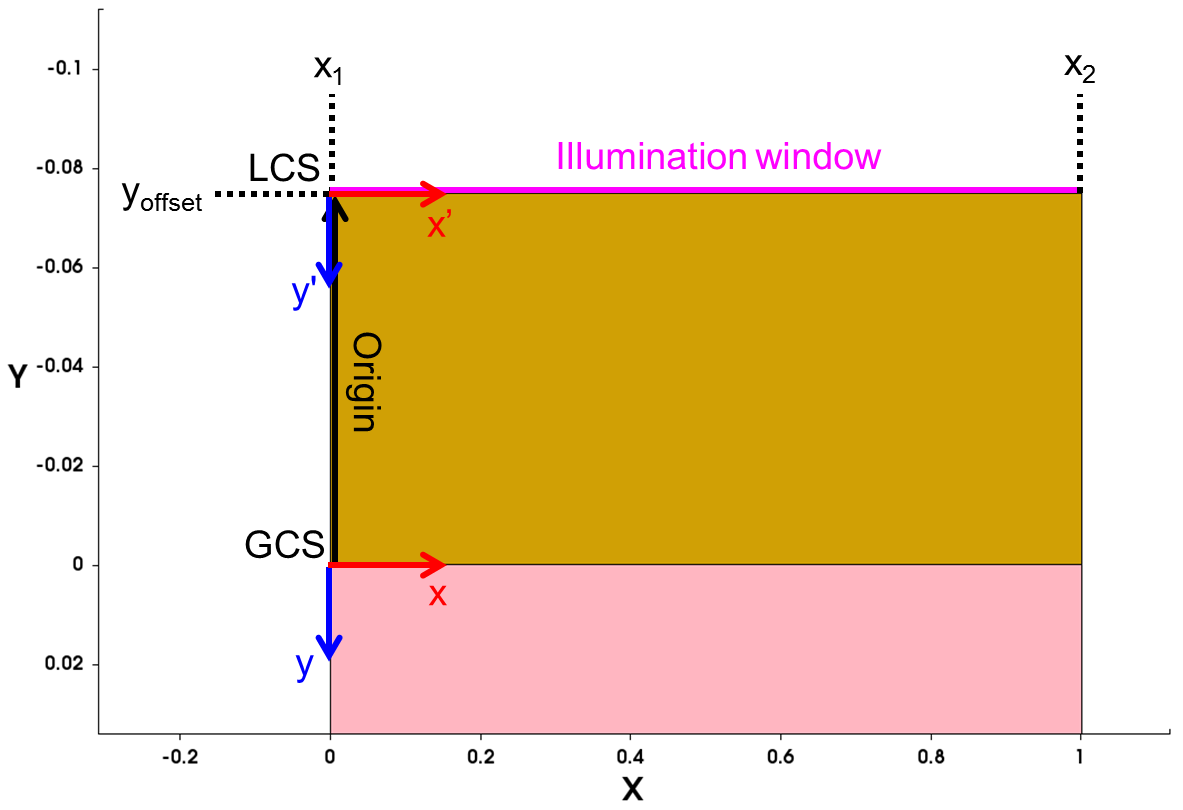
In this example, the SiN layer of the structure starts at y=-@dSiN@, where the Sentaurus Workbench parameter @dSiN@ defines the SiN layer thickness and has a value of 0.075. Since light will fall on top of the SiN layer, the origin of the LCS must be shifted up by @dSiN@. This is achieved by setting Origin=(0,-@dSiN@).

The Line command defines the start point and the endpoint of the illumination window in the LCS. Here, the entire width of the structure from x1=0 to x2=1 is illuminated (see Figure 3).

Structure with illumination window

Figure 3. Defining the illumination window in a 2D structure. (Click image for full-size view.)

The excitation direction is defined with respect to the GCS and is independent of the illumination window orientation.

5.2.4 OpticalSolver Section

The solver and solver-specific settings are defined in the OpticalSolver section. Only one solver is allowed.

In this example, TMM is used:

      TMM (
        LayerStackExtraction(
          Medium(
            Location = Bottom
            Material = "Silicon"
          )
        ) * end LayerStack
      ) * end TMM

As TMM is a 1D solver, you must instruct Sentaurus Device from where it must extract the 1D layer stack. This is done using the LayerStackExtraction command, which by default creates an extraction line in the center of the illumination window and perpendicular to the illumination window, in the same direction as light falls through the illumination window. In this example, the layer stack extraction starts at (0.5,-@dSiN@) and points downwards in the +y-direction.

HINT When setting up the simulation, always check the illumination window settings in the log file:

IlluminationWindow("unnamed_0"):
Origin: (0.0000e+00, -7.5000e-02, 0.0000e+00)
XDirection: (1, 0.0000e+00, 0.0000e+00)
LayerStackExtraction("unnamed_0"):
Position of starting point: (0.5, -7.5000e-02, 0.0000e+00)
Direction of extraction line: (-0.0000e+00, 1, 0.0000e+00)

as well as the extracted layer stack itself:

Multilayer Structure:
---------------------
Layer | Thickness [um] |      n |         k | alpha [cm^-1] |  mean abs [1]
    0                0   1.0000   0.000e+00       0.000e+00       0.000e+00
    1            0.075   2.1542   0.000e+00       0.000e+00       0.000e+00
    2                2   5.0042   4.161e+00       1.743e+06       4.137e-01
    3                0   5.0042   4.161e+00       1.743e+06       0.000e+00

Later in this example, you will want to neglect any reflection from the rear side, assuming a very thick (semi-infinite) silicon substrate. This can be achieved with the Medium command, by explicitly specifying the semi-infinite region at the bottom of the TMM stack as silicon.

5.2.5 Solve Section

In this example, you want to solve only optics without any other electrical equation. This is achieved using the keyword Optics.

In addition, optics will be solved for several wavelengths. In this case, it should be computed for the wavelength range @wstart@ to @wend@, using @wsteps@ steps. As any parameter defined in the Optics section can be ramped in the Quasistationary statement, the following lines will do this:

  Quasistationary (  
    DoZero
    InitialStep = @<1./wsteps>@ MaxStep = @<1./wsteps>@ Minstep = @<1./wsteps>@
    Goal { modelParameter="Wavelength" value=@wend@ }
  ) {
    Optics
  }

The step size is fixed by setting InitialStep, MaxStep, and MinStep to 1/@wsteps@. The start wavelength @wstart@ is specified in the Excitation section, while the end wavelength @wend@ is specified in the Goal statement.

5.2.6 Plotting the Results

Different solvers can output different results. In the case of TMM, the reflection, the transmission, and the total absorption are directly available in the .plt file.

To plot against wavelength, the wavelength must be added to the .plt file. This is done in the Sentaurus Device command file by adding Wavelength to the CurrentPlot section:

CurrentPlot{
  ModelParameter="Wavelength"
}

With this, the reflection curve can be created easily with the following lines in Sentaurus Visual:

set n @previous@
set proj "n${n}_des.plt"
set varWavelength "Device=,File=CommandFile/Physics,DefaultRegionPhysics,"
set varWavelength "${varWavelength}ModelParameter=Optics/Excitation/Wavelength"
set varR "LayerStack(unnamed_0) R_Total"

set ds($n) [load_file_datasets $proj]

create_curve -name R($n) -dataset $ds($n) -axisX $varWavelength -axisY $varR

Click to view the complete command file svisual_vis.tcl.

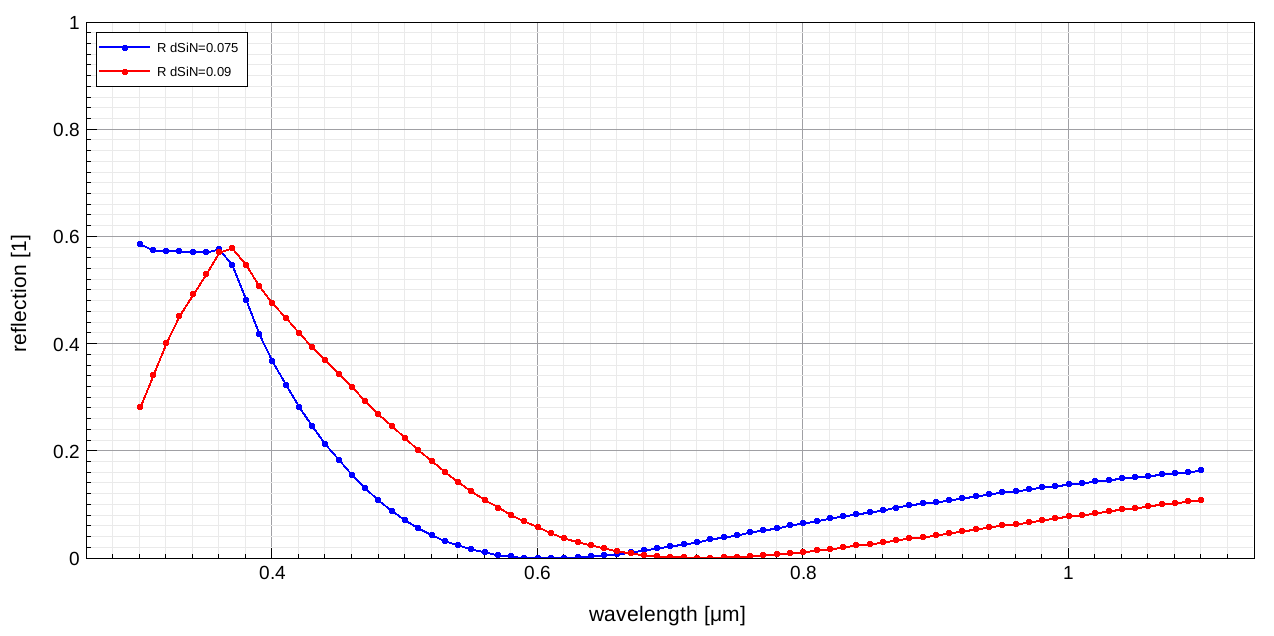
Finally, clicking the Run Selected Visualizer Nodes Together toolbar button generates the required reflection versus wavelength plot (compare Section 6.5 Visualize Selected Nodes Together). The minimum of the reflection has shifted as the thickness of the SiN coating changes (see Figure 4).

Plot of reflection versus wavelength

Figure 4. Reflection versus wavelength for two different SiN thicknesses using TMM. (Click image for full-size view.)

5.3 Calculating Angular-Dependent Reflection Using Raytracing

In this section, the basics of using the raytracer are explained with a simple 2D example that calculates the reflectance of a planar semi-infinite silicon substrate for different angles of incidence. The calculation is purely optical; no electrical equations are solved. Therefore, optical generation is of no interest here.

The complete project can be investigated from within Sentaurus Workbench in the directory Applications_Library/GettingStarted/sdevice/opto/rt-angular-r.

5.3.1 Boundary Conditions at Interfaces

In Sentaurus Device, an interface is defined as the face (3D) or the edge (2D) of two adjacent regions. For each interface, where boundary conditions (BCs) other than the default Fresnel BC are required, you must define the BC as to how the raytracer will propagate any impinging ray. As a consequence, care must be taken when setting up the device structure, such that all interfaces of special interest actually have two adjacent regions.

Click to view the complete command file sde_dvs.cmd.

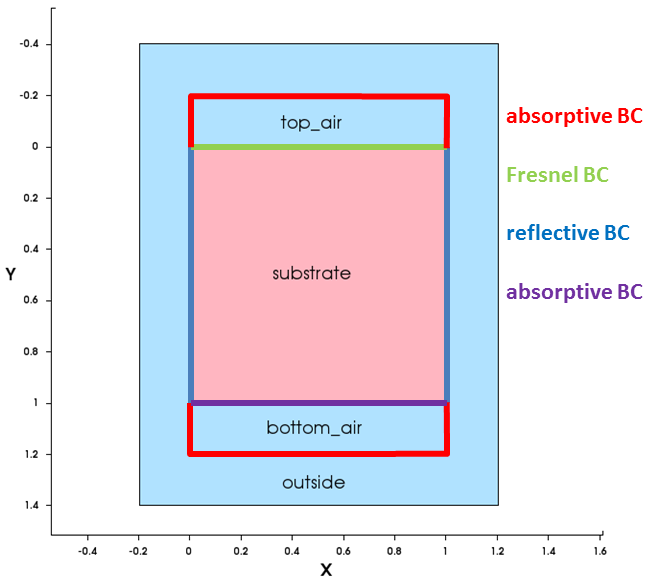
In this example, the following BCs are used (see Figure 5):

Boundary conditions for the raytracer

Figure 5. Boundary conditions for the raytracer. (Click image for full-size view.)

To control the BC for a particular interface, a region or material interface Physics section is used:

Physics (RegionInterface="region1/region2") {RaytraceBC(...)}
Physics (MaterialInterface="material1/material2") {RaytraceBC(...)}

The order of the regions to name the interface is not important, that is, region1/region2 and region2/region1 are equivalent.

By default, an interface behaves according to Snell's law and Fresnel equations. This case is called the Fresnel BC. However, other BCs are of interest as well. Commonly used BCs are:

This results in the following BC settings for the example:

* absorptive BC at the side walls of Si
Physics(RegionInterface="substrate/outside") {
  RayTraceBC (Reflectivity=1)
}
* absorptive BC at the bottom of Si
Physics(RegionInterface="substrate/bottom_air") {
  RayTraceBC (Reflectivity=0 Transmittivity=0)
}
* absorptive BC for the rest
Physics(MaterialInterface="Gas/Gas") {
  RayTraceBC (Reflectivity=0 Transmittivity=0)
}

Click to view the command file sdevice_des.cmd.

5.3.2 Common Optical Solver Settings

The general setup is very similar to the example in Section 5.2 Calculating Wavelength-Dependent Reflection by TMM. However, some specific settings are explained here.

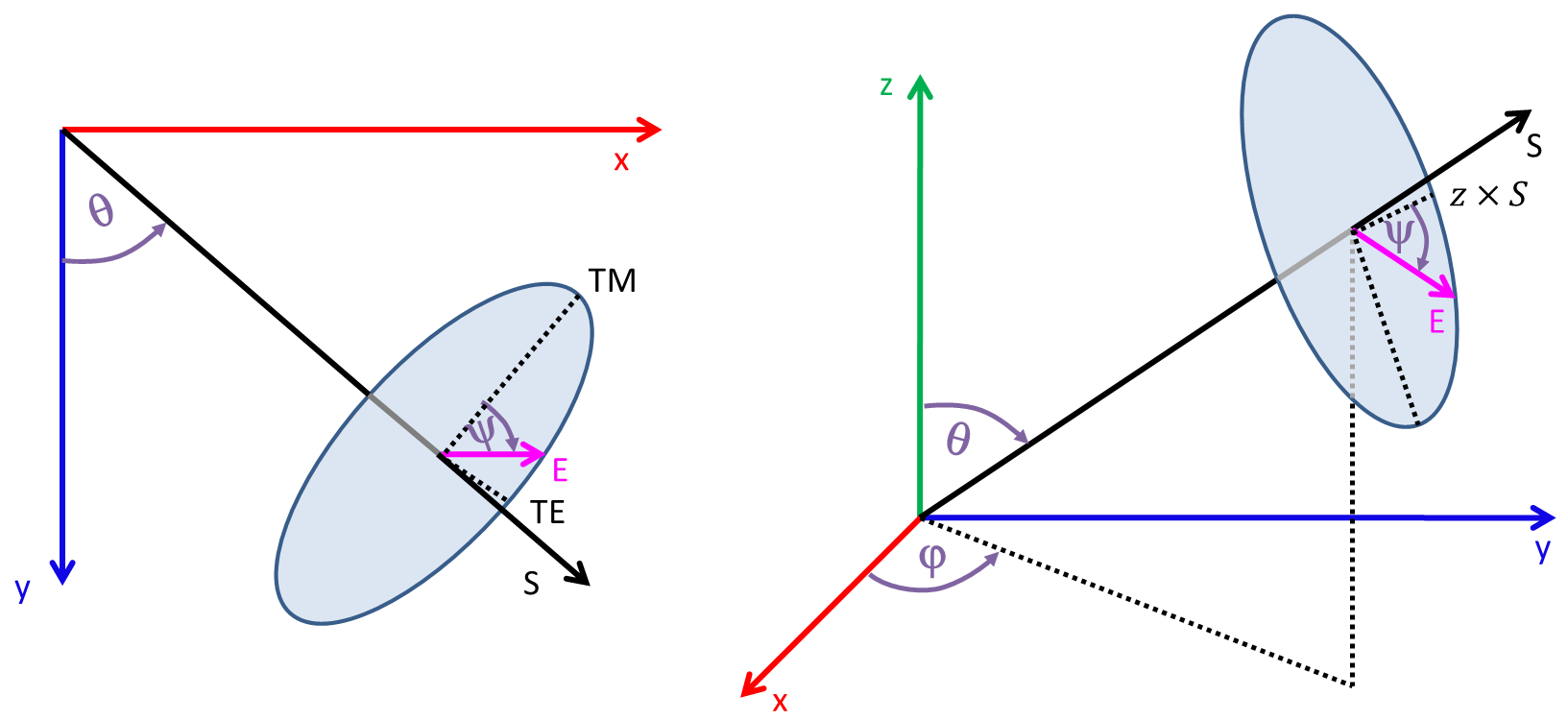
In contrast to the previous example, you want to change the incident angle of the light θ using the keyword Theta in the Excitation section, which in two dimensions defines the angle between the incident light direction and the +y-axis with counterclockwise orientation (see Figure 6).

Angle definition for excitation in two and three dimensions

Figure 6. Angle definition for excitation direction and polarization in (left) two dimensions and (right) three dimensions. (Click image for full-size view.)

The excitation angle is defined with respect to the GCS and not with respect to the illumination window.

The polarization of the excitation is characterized by the polarization angle Ψ and can be set with the PolarizationAngle keyword:

Optionally, instead of PolarizationAngle, the Polarization keyword can be used, with Polarization = sin2(PolarizationAngle).

For convenience, in two dimensions, pure TE and TM polarization can be specified with Polarization=TE or Polarization=TM.

In three dimensions, an additional angle Phi is used to define the excitation direction, and the polarization can be specified using PolarizationAngle only.

This example uses the DF–ISE coordinate system in two dimensions, where the +y-axis points downwards. Therefore, Theta=0 is perpendicular to the device top surface, and Theta=90 is parallel.

Similar to the wavelength sweep in the previous example, you now want to perform an angular sweep, which is achieved by:

5.3.3 Raytracer-Specific Settings

Some important commands control the raytracer are specified in the OpticalSolver(Raytracing(...)) section.

First, the starting rays must be distributed inside the illumination window. Several algorithms do this such as AutoPopulate, Equidistant, and MonteCarlo (refer to the Sentaurus™ Device User Guide for details). However, the easiest to start with is AutoPopulate, where only the number of rays must be specified:

        RayDistribution(
          Mode=AutoPopulate
          NumberOfRays = 1
        )

As the structure is planar and only reflection is of interest, one ray is sufficient.

Second, break criteria must be defined to control when tracing of a ray will be terminated. For this purpose, the raytracer provides two criteria:

        MinIntensity = 1e-4
        DepthLimit = 10000

MinIntensity stops the tracing of a ray if the ray intensity reaches the specified relative limit. In the above example, rays stop if their intensity becomes less than 1e-4 times their original intensity. DepthLimit stops the ray if it passes through more than the given number of interfaces.

MinIntensity is a more physical criterion that ensures correct results, while DepthLimit is more like an emergency break to avoid infinite loops for rays that are trapped in the structure and are never absorbed.

5.3.4 Calculating the Reflection

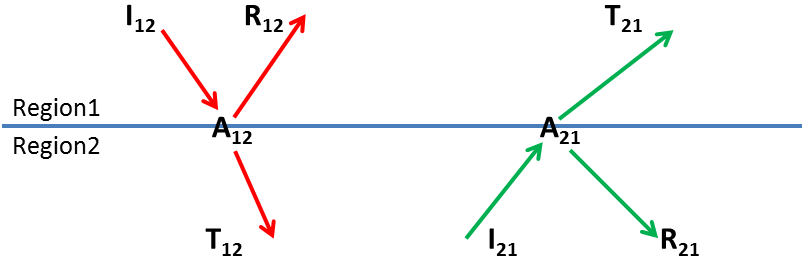
To extract optical quantities such as reflection or transmission, the raytracer can integrate photon fluxes across interfaces. To use this feature for a particular interface, the keyword PlotInterfaceFlux must be present in the RayTracing section. In addition, a BC must be defined for that interface. After this, for each region interface and impinging direction, Sentaurus Device plots the reflected, transmitted, and absorbed flux into the .plt file (see Figure 7).

Calculating the reflection using the raytracer

Figure 7. Calculating the reflection using the raytracer. (Click the image for full-size view.)

Therefore, at each interface, you can calculate the incident photon flux using the formula:

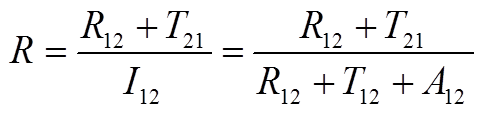
Formula for incident photon flux

For this example, the reflection, which is the number of reflected photons Nr divided by the number of impinging photons Nin, will be calculated in Sentaurus Visual.

Nr can be extracted using two different methods:

  1. As the absorbed photon flux of the top_air/outside interface.
  2. As the reflected photon flux of the top_air/substrate interface plus the transmitted photon flux of the substrate/top_air interface.

For Nin, you can do one of the following:

The calculation using method 1 for Nin and Nr in Sentaurus Visual looks like:

#- calculate reflection from input photons and absorbed photons 
#- at top_air/outside interface
create_curve -name Nin1 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytracePhoton Input" ;# 1/s
create_curve -name Nr1  -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux A(top_air/outside)" ;# 1/s
create_curve -name R1($n)  -function "<Nr1>/<Nin1>"

Using method 2 in Sentaurus Visual looks like:

#- calculate reflection from top_air/substrate interface only
create_curve -name tmp1 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux R(top_air/substrate)" ;# 1/s
create_curve -name tmp2 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux T(top_air/substrate)" ;# 1/s
create_curve -name tmp3 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux A(top_air/substrate)" ;# 1/s
create_curve -name Nin2  -function "<tmp1>+<tmp2>+<tmp3>"

create_curve -name tmp4 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux R(top_air/substrate)" ;# 1/s
create_curve -name tmp5 -dataset $ds($n) -axisX $varTheta \
	-axisY "RaytraceInterfaceFlux T(substrate/top_air)" ;# 1/s
create_curve -name Nr2  -function "<tmp4>+<tmp5>"
create_curve -name R2($n)  -function "<Nr2>/<Nin2>"

The first region name in the interface name (for example, R(top_air/substrate)) denotes the region from where the ray originated before reaching the interface.

Click to view the complete command file svisual_vis.tcl.

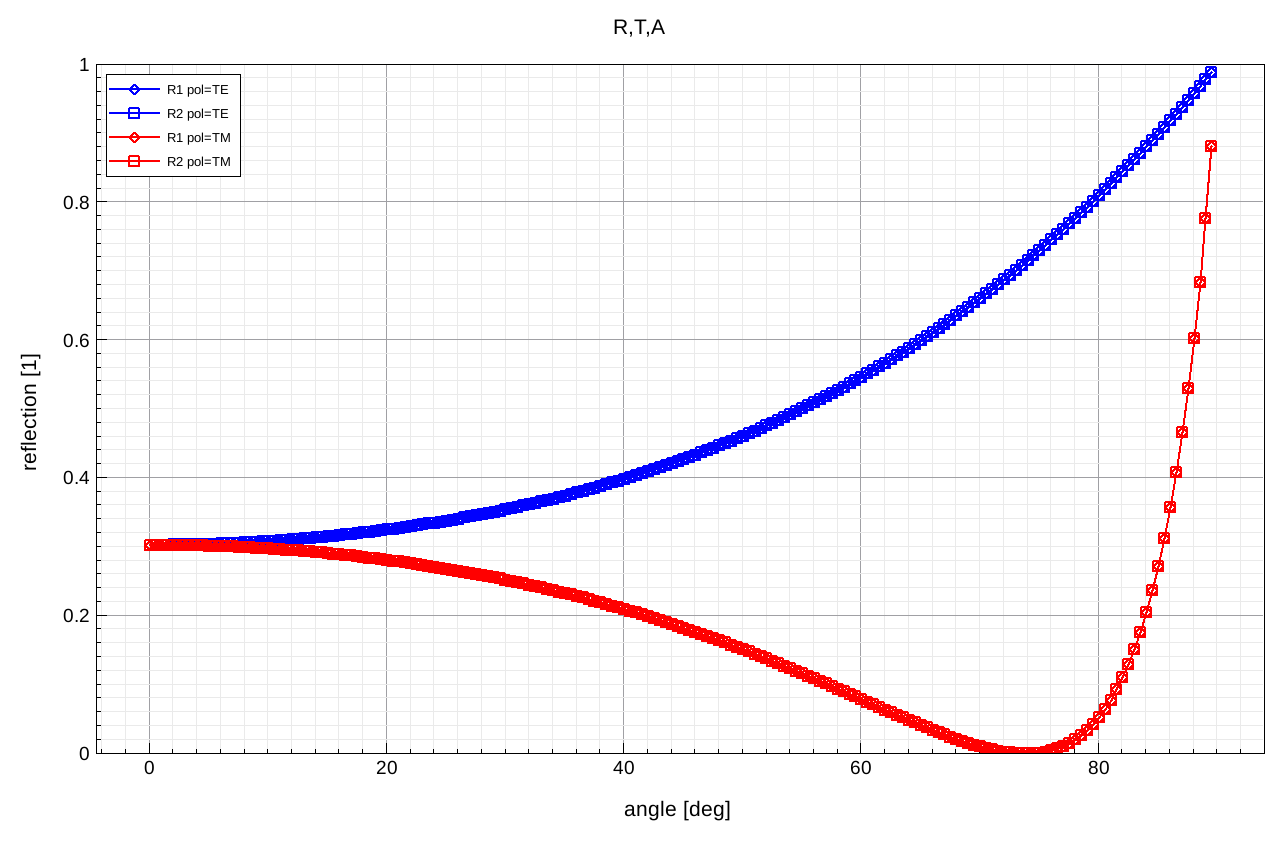
Finally, clicking the Run Selected Visualizer Nodes Together toolbar button generates the required reflection versus incident angle plot (compare Section 6.5 Visualize Selected Nodes Together). The reflection calculated according to the first and second methods as previously described are identical as expected (see Figure 8).

Plot of reflection versus incident angle

Figure 8. Reflection versus incident angle for TE and TM polarization using the raytracer. (Click image for full-size view.)

5.4 Calculating the White Light Photocurrent of a 3D Photodiode Using Raytracing

This section discusses combined optical and electrical equations, and addresses spectral illumination. As an example, the short-circuit current of a 3D photodiode illuminated with the standard solar spectrum AM1.5g is calculated using the raytracer. To optimize light coupling, the light-exposed silicon will be covered by a single nitride layer, which serves as an antireflective coating.

The complete project can be investigated from within Sentaurus Workbench in the directory Applications_Library/GettingStarted/sdevice/opto/rt-jsc-3d.

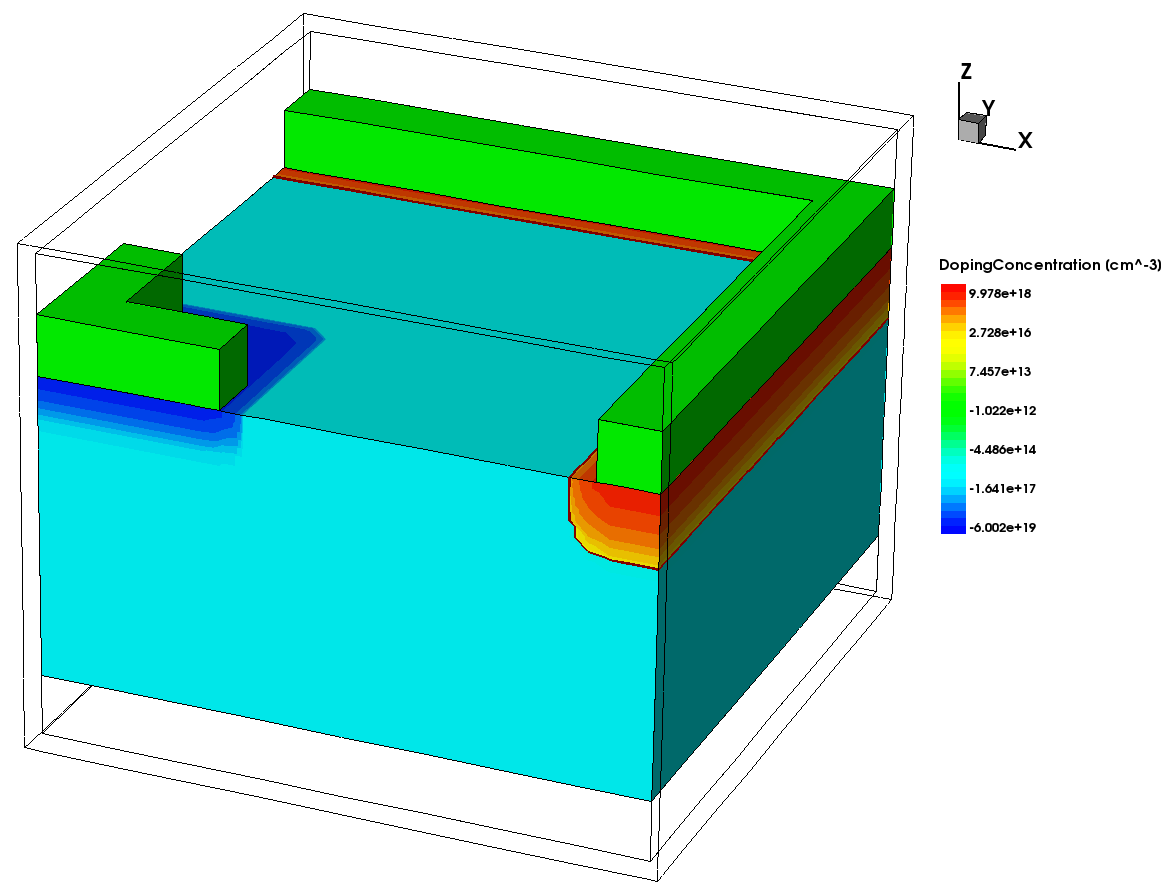
Similarly as in Section 5.3 Calculating Angular-Dependent Reflection Using Raytracing, a top_air region and a bottom_air region are added to the structure, and the entire device is surrounded by an air region. This is done to give access to the boundary conditions of the top, bottom, and sidewalls (see Figure 9) by specifying interface Physics sections in the Sentaurus Device command file.

Photodiode boundary

Figure 9. Boundary and doping of the 3D photodiode. Note the black wireframe that marks the surrounding region needed to define boundary conditions. (Click the image for full-size view.)

5.4.1 TMM Boundary Condition

To improve light coupling, antireflective coatings are widely used. These layers are typically in the range of wavelength, therefore, interference effects are crucial. On the other hand, they are typically electrically inactive, so they do not contribute to the optical generation and can be neglected in the electrical simulation.

A common approach to model such thin coatings with the raytracer is to collapse the coating layers onto the interface, and then to calculate the reflection and transmission coefficients using TMM.

In the example, at the top_air substrate interface, a 75 nm thick nitride is defined with the lines:

Physics (RegionInterface="top_air/substrate") {
  RayTraceBC(
    TMM(
      ReferenceRegion = "top_air" 
      LayerStructure {
        75e-3 "Nitride"
      }
    )
  )
}

Click to view the complete command file sdevice_des.cmd.

5.4.2 Computing Optical Generation From Spectrum

In contrast to the previous examples, now you will illuminate the device with a complete spectrum. The spectrum is defined in a separate file and is set in the File section:

File {
  IlluminationSpectrum = "am15g.txt"
}

The spectrum file usually consists of a list of wavelength and intensity pairs:

#- $Id: //tcad/support/main/modules/pardb/spectra/am15g.txt#6 $
# AM 1.5 global solar spectrum according to ASTM IEC904-3
# intensity = 0.1 W/cm2
# integration has to be performed according to Sum(y_i)
wavelength [um] intensity [W*cm^-2]
+3.0750000e-01 +1.2986361e-05 
+3.1250000e-01 +3.7582516e-05 
+3.1750000e-01 +7.2282062e-05 
...

In Sentaurus Device, a spectrum file has a much more general meaning than "a list of wavelengths and intensities". It basically defines an intensity depending on one or several other parameters. Therefore, it can consist of an arbitrary number of columns plus one intensity column. Examples would be a wavelength-dependent and angular-dependent spectrum, or an angular intensity distribution in three dimensions depending on two angles.

The units of the entries can be changed in the header line so that you can easily read in data in other units without having to rescale the data. For example, to read in wavelengths in nanometers and intensity in mW/m2, use:

wavelength [nm] intensity [mW*m^-2]

To activate spectral illumination, you must specify ComputeFromSpectrum in the OpticalGeneration(...) section. Sentaurus Device then computes the optical generation profiles for all wavelengths using the corresponding intensities and sums them to form a single profile, the white light optical generation profile.

When summing the different optical generation profiles, it is important to use an adequate quantum yield model. In this case, the StepFunction(EffectiveBandgap) model has been chosen, which assumes that each absorbed photon with an energy larger than the effective band gap creates an electron–hole pair. Otherwise, no carriers are generated.

Consequently, as you are interested only in the wavelength range that produces charge carriers, the computation of wavelengths larger than the effective band gap can be omitted. To select the spectral range of interest, use the following Select statement in the ComputeFromSpectrum section:

      ComputeFromSpectrum(
        Select(
          Parameter= ("Wavelength")
          Condition = "$wavelength <= 1.2"
        )
      ) * end ComputeFromSpectrum

Here, Parameter defines the list of column names from the spectrum file that are used in the Select statement. Condition is a string forming a valid Tcl expression, where identifiers preceded by a dollar sign ($) refer to the respective column in the spectrum file. Therefore, the above condition selects all entries from the spectrum file with a wavelength smaller than or equal to 1.2 μm.

Identifiers without a preceding dollar sign refer to a Sentaurus Device parameter.

5.4.3 Illumination in Three Dimensions

As the device coordinate system is the unified coordinate system (UCS), the top of the device is in the -x-direction. To illuminate the device from the top, the excitation direction must be in the +x-direction. This is achieved by setting Theta=90 and Phi=0 in the Excitation section (see Figure 6):

    Excitation (
      Theta=90 * angle of incidence from +z to +x axis
               * 0 points in +z direction, 90 in +x direction.
      Phi=0    * second rotation of excitation direction from +x to +y around z
               * e.g. with theta=90, phi=0 points in +x direction, phi=90 in +y.
      ...
    )

Figure 10 illustrates the alignment of the illumination window with the device. The illumination window must cover the entire device slightly above the top of the metal contacts.

Alignment of illumination window with the device

Figure 10. Alignment of the illumination window with the device. (Click image for full-size view.)

To accomplish this, the origin of the LCS (compare Section 5.2 Calculating Wavelength-Dependent Reflection by TMM) has shifted horizontally to the center of the device (2.5, 2.5), where the total width of the device is 5 μm and 1.2 μm above the silicon surface:

      Window ( 
        Origin = (-1.2, 2.5, 2.5)
        xDirection=(0,0,1)
        yDirection=(0,1,0)
        Rectangle(dx=5 dy=5)
      ) * end window

Next, the LCS (x', y') is rotated such that x' points in the z-direction and y' points in the y-direction of the GCS. This is achieved with the xDirection and yDirection commands (see Figure 2).

The width of the illumination rectangle in the x-direction and y-direction is specified with the keywords dx and dy. If relative parameters such as dx are chosen to define the geometry extent, instead of absolute parameters such as corner1 (or x1 in two dimensions), the illumination window geometry is positioned such that the center of the geometry is at the origin of the LCS. As the origin of LCS is at (2.5, 2.5) and the rectangle extends 5 μm in each direction, the entire area from (0, 0) to (5, 5) is covered by the illumination window.

Distribution of the rays, in this case, is performed in Equidistant mode, specifying the distance between the starting rays in the x-direction and y-direction:

        RayDistribution(
          Mode=Equidistant
          Dx=0.5
          Dy=0.5
        )

In the case of 3D simulations, the number of rays might increase rapidly and, with this, also the elements in the raytree increase exponentially. Therefore, the computer memory will limit the simulation. To work around memory limitation, you can specify the option CompactMemoryOption in the Raytracing(...) section, which reduces the memory need dramatically, due to sequential computation. However, plotting of the raytree is not available with this option.

Another way to optimize runtime and memory usage is to use a different tracing algorithm. By default, a deterministic algorithm is used. This means that, whenever a ray hits an interface, the ray is split into a reflected ray and a transmitted ray, and both of them are followed until they leave the device or a break criterion is met.

To change from an exponential behavior to a more efficient linear behavior, the raytracer offers the MonteCarlo algorithm. In this case, whenever a ray hits an interface, either the reflected ray or the transmitted ray is followed, depending on a random number, weighted with the reflection and transmission coefficients. Therefore, if an interface has 30% reflectance, three rays out of 10 rays will be reflected, and seven will be transmitted.

5.4.4 Extracting Results

The simulation is run by solving electrical equations only. Nevertheless, optics are solved because when Sentaurus Device is instructed to solve the transport equations for electron and holes, it detects that the optical generation term is not updated and will call the optical solver to update it. Therefore, no explicit call of the Optics section is necessary in this case.

Depending on the device structure and optical injection level, convergence might be problematic if the device is overwhelmed with optically generated carriers from the beginning. It is advisable to first solve transport in the dark, and only then switch on the light. This can be achieved by setting scaling=0 in the OpticalGeneration section:

    OpticalGeneration (
      Scaling=0
    ...)

In the Solve section, you first solve transport in the dark:

Solve{
  NewCurrentFile="tmp_"
  Poisson
  Coupled (Iterations=100) { poisson electron hole  }

Note that you have redirected the current file to tmp_n@node@_des.plt as these temporary preiterations are not required in the final results.

Then, you switch on the light by ramping the scaling parameter to the required value:

  Quasistationary ( 
    InitialStep= 1e-1 MaxStep= 0.5
    Goal { ModelParameter= "Scaling" Value= 100 }
  ){
    Coupled {Poisson Electron Hole}
  }

In the end, you switch back the current file to n@node@_des.plt and recalculate the required illuminated short-circuit current:

  NewCurrentFile=""
  Coupled { poisson electron hole }

As a result, the photogenerated current jph is extracted by integrating the optical generation inside the semiconductor region, and the short-circuit current jsc at the contact with a Sentaurus Visual node. The results are returned to Sentaurus Workbench (see Figure 11).

Click to view the complete command file svisual_vis.tcl.

Snapshot of Sentaurus Workbench project

Figure 11. Snapshot of Sentaurus Workbench project.

main menu    |   module menu    |   << previous section    |   next section >>